Bike Stability – Good or bad?

Bicycle Front-End Geometry Explained

Why a stable bike weaves at low speed and when climbing 

By Lennard Zinn

We all want a stable bike, right? Seems like a no-brainer. A bicycle that feels rock solid going downhill can form the foundation for a great feeling of security and more confidence at high speeds than you felt on less stable bikes. Thing is, there is a tradeoff between high-speed stability and low-speed control. 

A stable bike ridden slowly will tend to weave; it will take more effort to keep it rolling in a straight line when pedaling gently around the neighborhood. For an elderly or inexperienced rider, this can be unnerving. 

Similarly, a mountain bike that allows you to ride faster down technical trails, absorbing bumps and keeping the wheels railing around the turns, will be harder to steer up a steep, technical climb; it will tend to veer toward one side of the trail or the other, especially when the tire encounters rocks and roots. The same bike that you felt so confident on going much faster down the same technical trails that you used to go slower on will have you dabbing your foot on climbs that you had cleaned many times before.

A modern-geometry trail mountain bike will have a very steep seat-tube angle and a very shallow head-tube angle. (The head tube is the tube in front that the fork goes through and pivots inside of; the seat tube is the tube the seatpost comes out of.) Its rear tire will be close to the bottom bracket (short chainstays), while the front tire will be way out in front, far from the bottom bracket, due to the fork extending forward at such a low angle. That front-end geometry makes it super stable at high speed. The larger the wheel/tire diameter, the more stable the bike will be, and that is not just because a bigger, heavier wheel has more rotational inertia keeping the bike upright in the same way a gyroscope does; it is also due to the way it changes the bike’s geometry.

Common trail-bike geometry these days is a 65.5-degree head-tube angle coupled to a suspension fork with 44mm of offset (fork rake). With, say, 29×2.4” tires, the bike’s “fork trail” is 121mm, which is huge. (I’ll explain fork trail in a moment; it has nothing to do with the fact that it’s a “trail bike” or that it’s ridden on trails.) With “29 Plus” (29×3.0”) tires, the fork trail grows to 125mm.

More importantly, that trail bike with 29×2.4” tires has a “wheel flop factor” of 46mm (48mm with 29+ tires). You never see wheel flop factor on geometry charts, and wheel flop best describes why the front tire will snake around on a steep, technical climb, tending to veer off and force you to put a foot down.

A bike designed for an elderly or inexperienced rider with a high handlebar and a short reach from saddle to bar will also have a shallow head angle, but rather than to make it stable for ripping down serpentine, rocky trails, it is to avoid toe overlap. The low angle of the fork keeps the front wheel further away from the bottom bracket so the feet won’t hit the tire when pedaling in a slow turn, which can cause an inexperienced or elderly rider to crash. 

Assuming a standard offset (rake) of the fork for hybrid bikes of around 47mm, the head angle will have to be well under 70 degrees to avoid toe overlap with big, comfortable tires (like 700x50C) and short reach to the handlebar (on a small bike, the effective horizontal top tube length would be perhaps 52cm). A bike with a 68-degree head angle and a fork with 47mm of rake has a fork trail of 95mm (that’s a lot) and a wheel flop factor of 33mm (also a lot).

To understand fork trail, look at the illustration at the left from my out-of-print Zinn’s Cycling Primer book. The fork offset, or fork rake, “R,” is the perpendicular offset of the center of the front hub from the steering axis. The head angle, “ø,” is the acute angle between the steering axis and the horizontal. The wheel radius is “r.” The fork trail, “T,” is the horizontal distance between the center of the tire contact patch and the intersection of the steering axis with the ground. It’s called fork trail, or just “trail,” because the tire’s contact point on the road trails behind the steering axis in the same way the little casters on a shopping cart do; the little forks on shopping cart front wheels flip around backward when you push the cart forward so the wheel trails the steering axis, and the forks flip around forward when you pull the cart backward, again so the wheel trails the steering axis. 

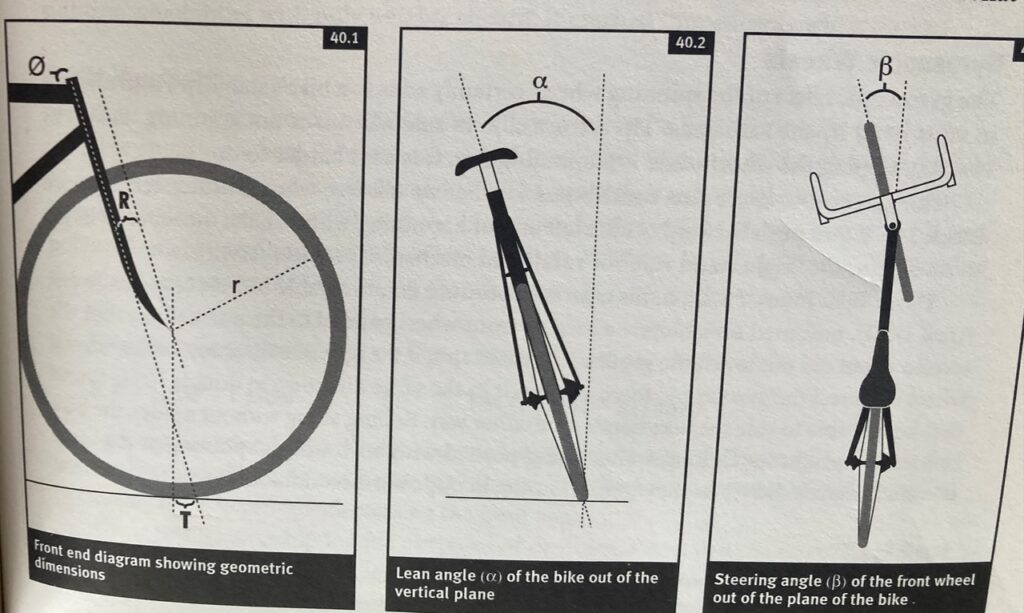
Simple trigonometry with those triangles in the illustration yields:

R = r*cosø – T*sinø

OR,      

T = (r*cosø – R)/sinø

The second equation clearly shows what you can see from the left illustration, namely that you can increase the fork trail by increasing the wheel radius, decreasing the rake, and/or decreasing the head angle. And for this discussion, you can decrease the fork trail by decreasing the wheel radius and/or increasing the rake (since you can’t do anything about your head angle). 

When you increase the fork trail, you also increase the bicycle’s stability, even though stability will probably not be the words used to describe the experience of a mountain biker climbing a steep, technical section on the trail bike or of the elderly rider pedaling the hybrid bike slowly around wide, neighborhood streets. 

Demonstrating what fork trail does for bike stability, if you were to pile weights on a bike and push it across a parking lot, the more fork trail it has, the longer it takes before it falls over, and the more it rights itself if you run alongside it and hit the handlebar to try and knock it over. If you roll the bike through a puddle, the wet track it leaves will weave all over the place as it slows down. That’s because the way the bike stays upright is to get the front wheel’s contact patch back under the bike’s center of gravity as fast as it can whenever the bike leans to the side, leading to increasingly dramatic swerving the slower it rolls.  

The middle illustration shows the lean angle ⍺, and the illustration on the right shows the steering angle, β. The bigger ⍺ is, the bigger β must be to correct the lean by getting the wheel back under the bike so it will stand back up again. 

You can demonstrate how decreasing the head angle will increase fork trail and stability and get insight into wheel flop at the same time. To simulate this with any bike, stack boxes under its front wheel (see top photo from that same book of mine). If you now lean the bike, you will see that the front wheel flops over into the turn to a much sharper angle than when it was flat on the floor, thus enabling the wheel contact patch to get back under the rider’s center of gravity more quickly.

Conversely, you can decrease fork trail and stability simply by increasing head angle. You can once again simulate this with your own bike, this time by stacking boxes under the rear wheel. Once the head angle is steep enough relative to the ground that the fork trail has become negative, when you lean the bike, the wheel will turn the opposite direction – away from the lean (bottom photo)! This means that when the unmanned, weighted bike rolling across the parking lot leans, its negative fork trail makes the front wheel turn the opposite way from the lean, thus moving its contact patch further out from under the bike’s center of gravity and causing it to crash immediately! 

The wheel flop you see in the top photo can be described mathematically as the amount the front end of the bike drops when the front wheel turns to the side. Where F = wheel flop factor, the bigger F is, the more the front end drops in a turn. 

F = T*sinø*cosø

For the trail bike, the sine of 65.5 degrees = 0.90996127087; the cosine of 65.5 degrees = 0.41469324265. For the hybrid bike, the sine of 68 degrees = 0.92718385456; the cosine of 68 degrees = 0.37460659341. Substituting those into this equation for wheel flop as well as the one further above for fork trail, you can see how I got the fork trails for those bikes of 121mm and 95mm and their wheel flop factors of 46mm and 33mm.

Both bikes have a large amount of wheel flop at low speed. While that high wheel flop factor gives them high speed stability, at low speed, it makes the bike wander wildly back and forth. The way you can decrease the wheel flop factor on those bikes is the same way you can decrease the fork trail—by decreasing the tire diameter and/or increasing the fork rake. 

If you put 27.5” or 26” wheels on the 29er trail bike, it would hold a line better while climbing; problem is, the rider would probably also hit the pedals on rocks. Substituting a suspension fork of the same length but with 51mm of offset (rake) rather than 44mm would decrease the bike’s fork trail from 121mm to 113mm and its wheel flop factor from 46mm to 43mm. 

You can decrease the tire radius on the hybrid bike by 25mm by switching from 700C wheels with 700x50C tires to 650B (27.5”) wheels with 650x42B tires; its fork trail would drop from 95mm to 85mm and wheel flop factor from 33mm to 29mm. Pedal strikes with the lower bottom bracket might not be an issue because of the slow riding and minimal lean angles in turns. A fork with 10-20mm more rake than that 47mm-rake fork would alleviate the low-speed weaving.

At high speed, both the aggressive trail bike and the high-handlebar hybrid bike will be super stable thanks to all that fork trail they have. The mountain biker on the trail bike will experience that stability when going fast down steep trails. The elderly or inexperienced rider on the hybrid will never experience high-speed stability when riding around neighborhoods and on flat bike paths.

A bike designer plays a dance between stability and instability to get desired performance out of a bike. For most mountain bikers, modern aggressive trail bikes don’t make a lot of sense. Swinging their design too far in the direction of high speed stability with high fork trail and big tires with high rotational inertia makes them tough to climb with. A bike that has a balance between high speed stability and low speed control is going to be more practical for 90% of mountain bikers. And building high-speed stability into a hybrid bike ridden at slow speeds also does not serve the rider.

As a frame builder, Lennard Zinn has been designing and building custom bicycles for over 42 years; he founded Zinn Cycles in 1982 and co-founded Clydesdale Bicycles in 2017. His Tech Q&A column on Substack follows his 35-year stint as a technical writer for VeloNews (from 1987 through 2022). He is a former U.S. National Cycling Team member and author of many bicycle books including Zinn and the Art of Mountain Bike Maintenance, Zinn and the Art of Road Bike Maintenance, and The Haywire Heart. He holds a bachelor’s degree in physics from Colorado College. 

Follow Lennard Zinn on Substack, Strava, X, Instagram, LinkedIn, or Facebook.